
With and, we now have a system of two equations in the variables ?b? and ?c?.Įliminate the parentheses, and combine like terms.Īctually, it isn’t impossible, but if something like that happens, it means that the original system of three equations has no solution. The advanced command allows you to specify whether you want approximate numerical answers as well as exact ones, and how many digits. Now we’ll subtract equation from equation. The Solve command can be uses to solve either a single equation for a single unknown from the basic solve page or to simultaneously solve a system of many equations in many unknowns from the advanced solve page. This time we need to multiply equation by ?4?, so we can subtract it from equation and eliminate the variable ?a?. We need to get another equation in only the variables ?b? and ?c?. 2x + y + 3z 0 Eliminate the same variable from each system: 4x - 3y + z - 10 2x +. Use arrayfun to apply char to every element. Now let’s subtract equation from equation, which will give us an equation in only the variables ?b? and ?c?.Įliminate the parentheses, and then combine like terms. Solving by Addition and Subtraction Pick two pairs: 4x - 3y + z - 10. Visualize the system of equations using fimplicit.To set the x-axis and y-axis values in terms of pi, get the axes handles using axes in a.Create the symbolic array S of the values -2pi to 2pi at intervals of pi/2.To set the ticks to S, use the XTick and YTick properties of a.To set the labels for the x-and y-axes, convert S to character vectors. The algorithms require calculation not only values of system equations at some point, but also the values of gradient, Jacobian or Hessian of. They realize well-known mathematical algorithms Newton-Raphson method, Levenberg-Marquardt method, Powell’s Dog Leg method and so on.

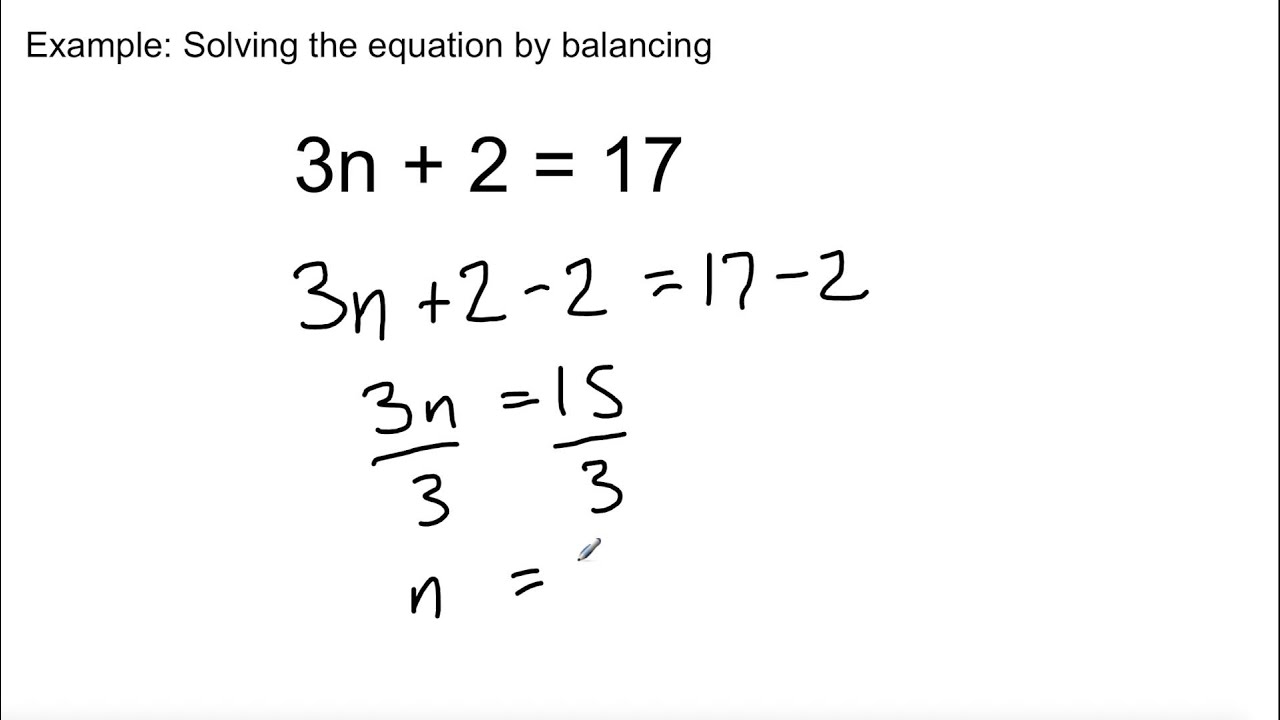
Next, take the second equation and replace y with 7-x, and. There are many libraries for solving nonlinear equation systems. Solve these systems of equations by elimination or substitution methods. Let’s multiply equation by ?3?, so we can eliminate the variable ?a? by subtracting the resulting equation from equation. Suppose we have the following linear system: We can take the first equation, x + y 7, and subtract x from both sides to get y 7 - x. This module includes exercises like evaluating the absolute value expression at a particular value, input and output tables, graph the absolute value function and solve the various types of absolute value equation. So we’ll need to multiply one of the equations by some number such that by combining the resulting equation with one of the other two equations, we’ll be able to eliminate a variable. None of the terms with the same variable have the same coefficient (or coefficients that are equal in absolute value but opposite in sign). Use any method to solve the system of equations. Remember that when you graph a line, you see all the different coordinates (or x/y combinations) that make the equation work. 1.50x + 0.50y 78.50 (Equation related to cost) x + y 87 (Equation related to the number sold) 4. Systems of linear equations and their solution, explained with pictures, examples and a cool interactive applet. The solution is ?(-1,-4,-4)? or ?x=-1?, ?y=-4?, and ?z=-4?. One equation will be related to the price and one equation will be related to the quantity (or number) of hot dogs and sodas sold. Now choose one of the three original equations, and plug in ?-1? for ?x? and ?-4? for ?z?, and then solve for ?y?. If we add these two equations, we can eliminate the variable ?z?, and then solve for ?x?.Ĭhoose one of the new equations, and plug in ?-1? for ?x?, and then solve for ?z?. The coefficients of ?z? in our two new equations are ?-2? and ?2?, respectively. You might have also noticed that the coefficients of ?y? in equations and are ?-5? and ?5?, respectively, so we can add these two equations to get another equation in only the variables ?x? and ?z?. Enter system of equations (empty fields will be replaced with zeros) x + y + z + t x + y + z + t x + y + z + t x + y + z + t Find approximate solution.

Remove parentheses and combine like terms. This calculator solves system of four equations with four unknowns.

If we add these two equations, the ?y? terms will cancel (we’ll eliminate the variable ?y?) and we’ll get an equation in only the variables ?x? and ?z?. You will also need to add or subtract any constants to both sides, and perform any other necessary operations.Notice that the coefficients of ?y? in equations and are ?-5? and ?5?, respectively. You will need to divide each side of the equation by the log of the exponential expression. To solve, you need to rewrite the equation so that one side contains the variable, and the other side contains all of the numbers.


 0 kommentar(er)
0 kommentar(er)
